Functions
Contents
Functions#
Lines, regions and surfaces#
We know that in \(\boldsymbol{R}^{2}\),
a single Cartesian equation represents a line or curve, e.g. \(x=2, y=2 x+1, x^{2}+y^{2}=9\)
a single inequality represents a region, e.g. \(x>2, x^{2}+y^{2} \leq 1\)
two equations represent the intersection of two curves, usually a point, e.g. \(x=2\) and \(y=2 x+1\) at the point \(x=2, y=5\).
In \(R^{3}\)
a single equation represents a surface
a single inequality represents a region
two equations represent the intersection of two surfaces, usually a curve.
Traces and Level Curves#
A trace is the cross-section of a surface with a plane.
For a surface \(z=f(x, y)\) we commonly consider vertical traces:
curves on which \(x=c_{1}\) and \(z(y)=f\left(c_{1}, y\right)\)
curves on which \(y=c_{2}\) and \(z(x)=f\left(x, c_{2}\right)\).
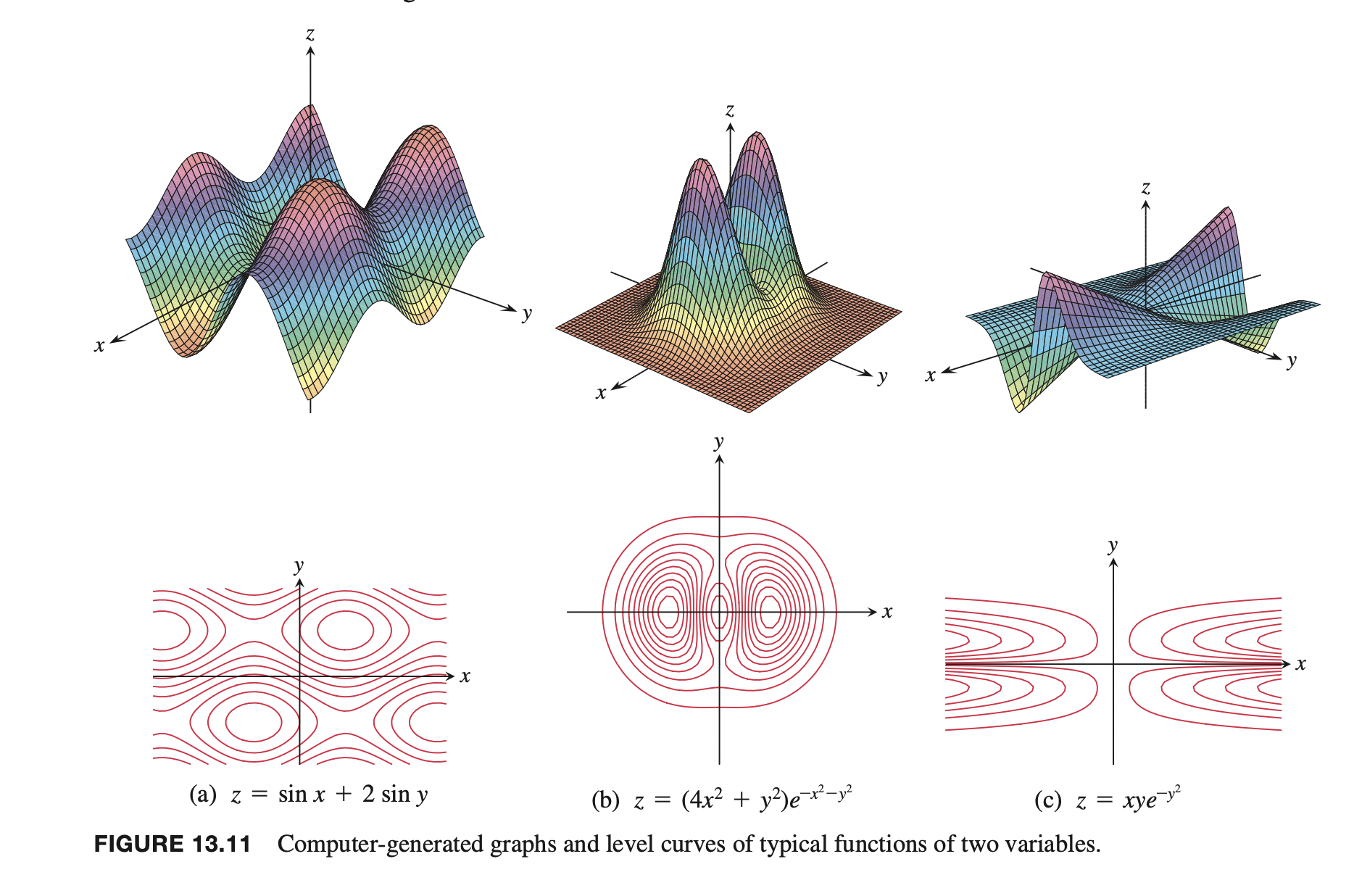
Horizontal traces \(z=f(x, y)=k\) are more often called level curves or contours. Note that if we lift contours and plot them at the appropriate heights, we get a picture of the surface itself.
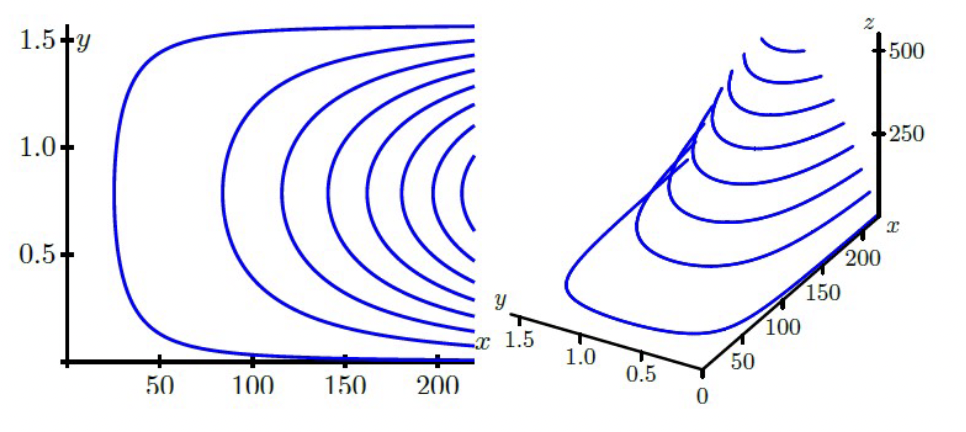
The set of points in the plane where a function \(f(x, y)\) has a constant value \(f(x, y) = c\) is called a level curve of \(f\). The set of all points \((x, y, f(x, y))\) in space, for \((x, y)\) in the domain of \(f\), is called the graph of \(f\). The graph of \(f\) is also called the surface \(z = f(x, y)\).
Functions of more variables#
A function \(f\) of three independent variables is a rule that assigns to each ordered triple \((x, y, z)\) in a domain \(D\) exactly one real number \(f(x, y, z)\) in a set \(R\).
A function \(f\) of \(n\) independent variables is a rule that assigns to each ordered \(n\)-tuple \(\left(x_{1}, x_{2}, \ldots x_{n}\right)\) in a domain \(D\) exactly one real number \(f\left(x_{1}, x_{2}, \ldots x_{n}\right)\) in a set \(R\).
Limits & Continuity#
Notions of limits and continuity are generally similar to the one-variable case except that a point in \(R^{2}\) can be approached along an infinite number of different paths.
If \(\lim _{(x, y) \rightarrow(a, b)} f(x, y)\) takes different values as \((a, b)\) is approached along two different paths then the limit does not exist.
\(f(x, y)\) is continuous at \((a, b)\) if and only if \(\lim _{(x, y) \rightarrow(a, b)} f(x, y)=f(a, b)\).
Graphically, a function is continuous where the surface has no break, hole or jump. For more details, see textbooks (or work on your own through Active Calculus 10.1)

