Second-Order Partial Derivatives and Chain Rule#

Second Derivatives#

A function \(f(x, y)\) has four partial derivatives:

\[\left(f_{x}\right)_{x}=f_{x x}=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right)=\frac{\partial^{2} f}{\partial x^{2}}\]
\[\left(f_{x}\right)_{y}=f_{x y}=\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right)=\frac{\partial^{2} f}{\partial y \partial x}\]
\[\left(f_{y}\right)_{x}=f_{y x}=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right)=\frac{\partial^{2} f}{\partial x \partial y}\]
\[\left(f_{y}\right)_{y}=f_{y y}=\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right)=\frac{\partial^{2} f}{\partial y^{2}}\]

Clairaut’s Theorem (The Mixed Derivative Theorem)#

Let \(f\) be a function of several variables for which the partial derivatives \(f_{x y}\) and \(f_{y x}\) are continuous near the point \((a, b)\). Then

\[ f_{x y}(a, b)=f_{y x}(a, b) . \]

Note: the mixed derivatives can be different when the continuity conditions are not satisfied.

Extensions of Clairaut’s theorem apply to higher partial derivatives and to functions of more variables. For example, for \(f(x, y)\) provided all the derivatives are continuous, we also have

\[ f_{x y z}=f_{x z y}=f_{y x z}=f_{y z x}=f_{z x y}=f_{z y x} \]

The Chain Rule (2 Variables)#

If \(z=f(x, y)\) where \(x=g(t)\) and \(y=h(t)\), then

\[ \frac{d z}{d t}=\frac{\partial z}{\partial x} \frac{d x}{d t}+\frac{\partial z}{\partial y} \frac{d y}{d t} \]

(provided the derivatives exist).

Proof in pg. 801

Tree Diagrams#

Chain rule can be helpfully represented using a tree diagram.

Note: Note carefully which derivatives are partial derivatives and which are ordinary derivatives.

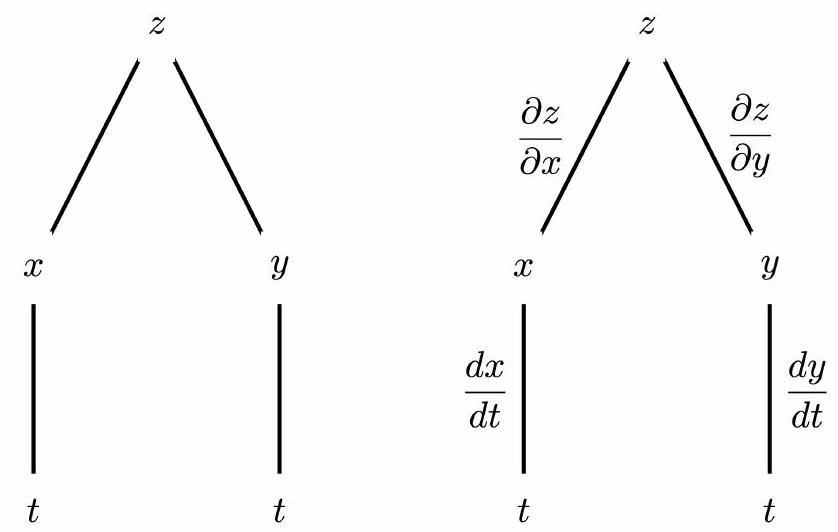
../../../_images/img2.jpg

The Chain Rule (General Version)#

If \(z=f\left(x_{1}, x_{2}, \ldots, x_{n}\right)\) and \(x_{i}=g\left(t_{1}, t_{2}, \ldots, t_{m}\right)\) then

\[ \frac{\partial z}{\partial t_{j}}=\frac{\partial z}{\partial x_{1}} \frac{\partial x_{1}}{\partial t_{j}}+\frac{\partial z}{\partial x_{2}} \frac{\partial x_{2}}{\partial t_{j}}+\ldots+\frac{\partial z}{\partial x_{n}} \frac{\partial x_{n}}{\partial t_{j}} \]

(provided the derivatives exist).

Implicit Differentiation#

  • If \(F(x, y)\) is differentiable and the equation \(F(x, y)=0\) defines \(y\) as a differentiable function of \(x\), then at any point where \(F_{y} \neq 0\),

\[ \frac{d y}{d x}=-\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial y}}=-\frac{F_{x}}{F_{y}} \]

  • If \(F(x, y, z)\) is differentiable and \(F(x, y, z)=0\) defines \(z\) as a differentiable function of \(x\) and \(y\), then at any point where \(F_{z} \neq 0\),

\[ \frac{\partial z}{\partial x}=-\frac{\frac{\partial F}{\partial x}}{\frac{\partial F}{\partial z}}=-\frac{F_{x}}{F_{z}} \quad \text { and } \quad \frac{\partial z}{\partial y}=-\frac{\frac{\partial F}{\partial y}}{\frac{\partial F}{\partial z}}=-\frac{F_{y}}{F_{z}} . \]

Differentiability#

pg. 796 Thomas’s Calculus