Double Integrals in Polar Coordinates

Polar coordinates

Conversions

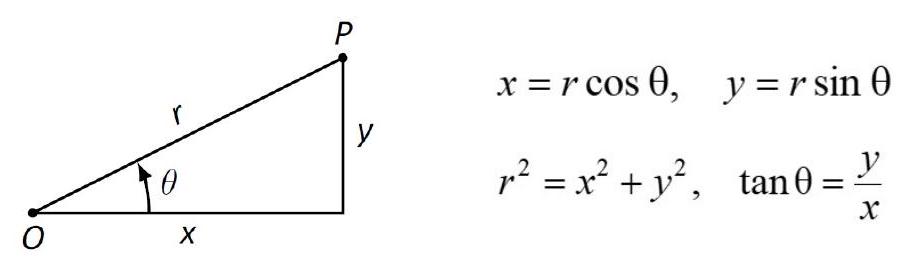
Note:

• For a given \((x, y)\), the equation \(\tan \theta=\frac{y}{x}\) has two solutions in the range \(0 \leq \theta \leq 2 \pi\). You must choose \(\theta\) so that the point lies in the correct quadrant, for examply by plotting the point.

• That is, you may need to take \(\theta=\arctan \left(\frac{y}{x}\right)\) or \(\theta=\arctan \left(\frac{y}{x}\right)+\pi\).

Double Integrals in Polar Coordinates

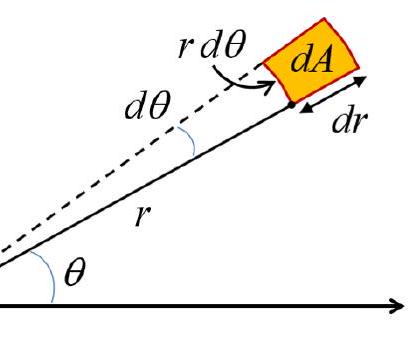
• The area element in Cartesian coordinates is \(d A=d x d y\).

• In polar coordinates it is \(d A=r d r d \theta\).

• Hence a double integral \(\iint_{D} f(x, y) d A\) in Cartesian coordinates can be converted to a double integral in polar coordinates \(\iint_{D} f(r \cos \theta, r \sin \theta) r d r d \theta\).

Note: Converting a double integral from Cartesian to polar coordinates is one example of performing a change of variables in a multiple integral. More generally, changes of variables are performed using what is known as a Jacobian - see Thomas section \(15.8\) (p953-958 cover the \(2 \mathrm{D}\) case).