Equation sheet#

Some combinations and identities#

The Laplacian#

  • For a scalar field \(f, \quad \nabla^{2} f=\vec{\nabla} \cdot \vec{\nabla} f=\frac{\partial^{2} f}{\partial x^{2}}+\frac{\partial^{2} f}{\partial y^{2}}+\frac{\partial^{2} f}{\partial z^{2}} \quad\) where \(\nabla^{2}\) is the Laplacian operator.

  • (It occurs in many important equations, such as the wave equation \(\nabla^{2} f-\frac{1}{c^{2}} \frac{\partial^{2} f}{\partial t^{2}}=0\), and as Laplace’s equation, the diffusion equation, the Schrödinger equation, etc.)

  • The Laplacian of a vector field \(\overrightarrow{\boldsymbol{F}}=M(x, y, z) \mathbf{i}+N(x, y, z) \mathbf{j}+P(x, y, z) \mathbf{k}\) is also defined:

\[ \nabla^{2} \overrightarrow{\boldsymbol{F}}=\nabla^{2} N \mathbf{i}+\nabla^{2} P \mathbf{j}+\nabla^{2} Q \mathbf{k} . \]

Curl Grad and Conservative Fields#

  • For any scalar field \(f(x, y, z)\) with continuous second derivatives, \(\vec{\nabla} \times \vec{\nabla} f=\overrightarrow{\mathbf{0}}\) (see Q17).

  • Hence for any conservative vector field \(\overrightarrow{\boldsymbol{F}}=\overrightarrow{\boldsymbol{\nabla}} f\) we have \(\overrightarrow{\boldsymbol{\nabla}} \times \overrightarrow{\boldsymbol{F}}=\overrightarrow{\mathbf{0}}\). That is, conservative fields are irrotational.

  • It can also be proved that if \(\vec{\nabla} \times \overrightarrow{\boldsymbol{F}}=\overrightarrow{\mathbf{0}}\) then \(\overrightarrow{\boldsymbol{F}}\) is conservative. This provides a simple test for whether a 3D field is conservative.

Some other identities#

  • There is a useful identity

\[ \vec{\nabla} \times(\vec{\nabla} \times \overrightarrow{\boldsymbol{F}})=\vec{\nabla}(\vec{\nabla} \cdot \overrightarrow{\boldsymbol{F}})-\vec{\nabla}^{2} \overrightarrow{\boldsymbol{F}} \]

  • For any vector field \(\overrightarrow{\boldsymbol{F}}, \quad \overrightarrow{\boldsymbol{\nabla}} \cdot(\overrightarrow{\boldsymbol{\nabla}} \times \overrightarrow{\boldsymbol{F}})=0 \quad\) (see Q19).

Theorem Summary#

FTC#

\[ \int_{a}^{b} F^{\prime}(x) d x=F(b)-F(a) \]

img

FTC for line integrals#

\[ \int_{C} \nabla f \cdot d \mathbf{r}=f(\mathbf{r}(b))-f(\mathbf{r}(a)) \]

img

Green’s theorem#

\[ \iint_{D}\left(\frac{\partial N}{\partial x}-\frac{\partial M}{\partial y}\right) d A=\oint_{C} M d x+N d y \]

img

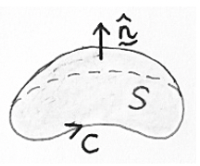
Stoke’s theorem#

\[ \iint_{S} \nabla \times \mathbf{F} \cdot d \mathbf{S}=\oint_{C} \mathbf{F} \cdot d \mathbf{r} \]

img

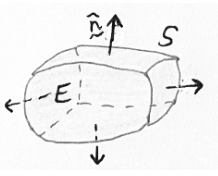
Divergence theorem#

\[ \iiint_{E} \nabla \cdot \mathbf{F} d V=\iint_{S} \mathbf{F} \cdot d \mathbf{S} \]

img