Triple Integrals in Cylindrical & Spherical Coordinates#

Cylindrical Coordinates#

A point \(P\) with Cartesian coordinates \((x, y, z)\) has cylindrical coordinates \((r, \theta, z)\) where \((r, \theta)\) are the polar coordinates of the point \((x, y)\) in the \(x y\)-plane and \(z\) remains unchanged (i.e. \(z\) is the directed distance of the point from the \(x y\)-plane).

  • The conversions are as for polar coordinates.

  • The differential volume element is \(d V=r d r d \theta d z\)

  • Cylindrical coordinates are especially useful for cylindrical regions, and when the integrand contains terms in \(x^{2}+y^{2}\).

Spherical Coordinates#

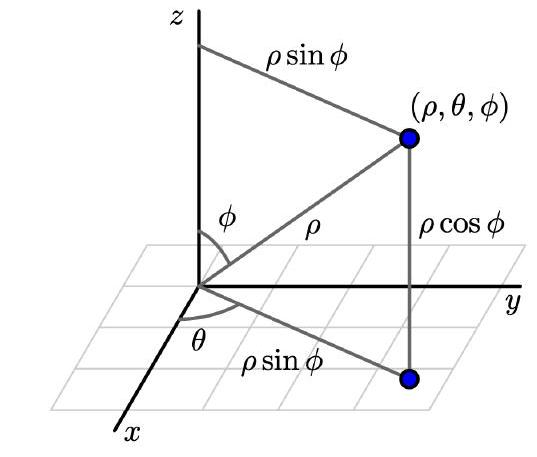
A point \(P\) with Cartesian coordinates \((x, y, z)\) has spherical coordinates \((\rho, \theta, \phi)\) where \(\rho\) is the distance from the point to the origin, \(\phi\) is the angle between \(\overrightarrow{O P}\) and the positive \(z\)-axis, and \(\theta\) is the angle between the \(x\)-axis and the projection of \(\overrightarrow{O P}\) onto the \(x y\)-plane (and is the same as \(\theta\) for the point in cylindrical coordinates).

  • To avoid multiple representations of a single point in space we restrict \(\rho \geq 0,0 \leq \phi \leq \pi\), and \(0 \leq \theta \leq 2 \pi\).

  • Conversions:

\[\begin{split} \begin{gathered} r=\rho \sin \phi, \quad x=r \cos \theta=\rho \sin \phi \cos \theta, \\ z=\rho \cos \phi, \quad y=r \sin \theta=\rho \sin \phi \sin \theta, \\ \rho=\sqrt{x^{2}+y^{2}+z^{2}}=\sqrt{r^{2}+z^{2}} . \end{gathered} \end{split}\]

  • The differential volume element is \(d V=\rho^{2} \sin \phi d \rho d \theta d \phi\).

  • Spherical coordinates are useful for regions bounded by spheres and cones, and when the integrand contains terms in \(x^{2}+y^{2}+z^{2}\).

Changes of Variables in Multiple Integrals#

Converting double integrals from Cartesian to polar coordinates, or converting triple integrals from Cartesian to cylindrical or spherical coordinates, are examples of performing a change of variables in a multiple integral.

The following more general results can be proved.

  • Suppose a change of variables \(x=x(s, t)\) and \(y=y(s, t)\) transforms a closed and bounded region \(R\) in the \(s t\)-plane into a closed and bounded region \(R^{\prime}\) in the \(x y\)-plane. Under modest conditions,

\[ \iint_{R^{\prime}} f(x, y) d A=\iint_{R} f(x(s, t), y(s, t))\left|\frac{\partial(x, y)}{\partial(s, t)}\right| d s d t \]

where

\[\begin{split} \frac{\partial(x, y)}{\partial(s, t)}=\frac{\partial x}{\partial s} \frac{\partial y}{\partial t}-\frac{\partial x}{\partial t} \frac{\partial y}{\partial s}=\left|\begin{array}{ll} \frac{\partial x}{\partial s} & \frac{\partial x}{\partial t} \\ \frac{\partial y}{\partial s} & \frac{\partial y}{\partial t} \end{array}\right| \end{split}\]

is known as the Jacobian. - Suppose a change of variables \(x=x(s, t, u), y=y(s, t, u), z=z(s, t, u)\) transforms a closed and bounded region \(E\) in the stu-plane into a closed and bounded region \(E^{\prime}\) in the \(x y z\)-plane. Under modest conditions,

\[ \iint_{E^{\prime}} f(x, y, z) d V=\iint_{E} f(x(s, t, u), y(s, t, u), z(s, t, u))\left|\frac{\partial(x, y, z)}{\partial(s, t, u)}\right| d s d t d u \]

using the Jacobian

\[\begin{split} \frac{\partial(x, y, z)}{\partial(s, t, u)}=\left|\begin{array}{lll} \frac{\partial x}{\partial s} & \frac{\partial x}{\partial t} & \frac{\partial x}{\partial u} \\ \frac{\partial y}{\partial s} & \frac{\partial y}{\partial t} & \frac{\partial y}{\partial u} \\ \frac{\partial z}{\partial s} & \frac{\partial z}{\partial t} & \frac{\partial z}{\partial u} \end{array}\right| \end{split}\]