Partial Derivatives#

Definition#

The partial derivatives of a function \(f(x, y)\) are:

\[ f_{x}(x, y)=\lim _{h \rightarrow 0} \frac{f(x+h, y)-f(x, y)}{h}, \quad f_{y}(x, y)=\lim _{h \rightarrow 0} \frac{f(x, y+h)-f(x, y)}{h} \]

  • To find \(f_{x}\) we differentiate \(f(x, y)\) with respect to \(x\), treating \(y\) as a constant.

  • To find \(f_{y}\) we differentiate \(f(x, y)\) with respect to \(y\), treating \(x\) as a constant.

Alternative notations for the partial derivatives of \(z=f(x, y)\) are

\[\begin{split} \begin{aligned} &f_{x}(x, y)=f_{x}=\frac{\partial f}{\partial x}=\frac{\partial}{\partial x} f(x, y)=z_{x}=\frac{\partial z}{\partial x} \\ &f_{y}(x, y)=f_{y}=\frac{\partial f}{\partial y}=\frac{\partial}{\partial y} f(x, y)=z_{y}=\frac{\partial z}{\partial y} \end{aligned} \end{split}\]
Thomas's Calculus

Partial Derivatives and Continuity#

A function \(f(x, y)\) can have partial derivatives with respect to both \(x\) and \(y\) at a point without the function being continuous there. This is different from functions of a single variable, where the existence of a derivative implies continuity.

Thomas's Calculus

\(f(x,y)\) consists of the lines \(L1\) and \(L2\) (lying 1 unit above the \(xy\)-plane) and the four open quadrants of the \(xy\)-plane. The function has partial derivatives at the origin but is not continuous there.

Partial derivatives of more variables#

Partial derivatives of functions of three or more variables are defined in a similar way. For example, for \(f(x, y, z)\) we have

\[ f_{x}(x, y, z)=\lim _{h \rightarrow 0} \frac{f(x+h, y, z)-f(x, y, z)}{h} \]

  • To find \(f_{x}(x, y, z)\) we differentiate \(f(x, y, z)\) with respect to \(x\), treating \(y\) and \(z\) as constants.

Tangent plane to the surface \(z=f(x, y)\) at the point \((a, b)\)#

If \(f\) is continuous and differentiable in an open disk containing the point \((a, b)\), the equation of the tangent plane is

\[ z=f(a, b)+f_{x}(a, b)(x-a)+f_{y}(a, b)(x-b) . \]

Linearization of \(f(x, y)\) at \((a, b)\)#

\[ L(x, y)=f(a, b)+f_{x}(a, b)(x-a)+f_{y}(a, b)(y-b) . \]

Near \((a, b)\) we may use the linear approximation \(f(x, y) \approx L(x, y)\).

Differentials and Small Changes#

Recall that in single variable calculus, if we have a differentiable function \(y=f(x)\) and \(x\) changes by \(d x=\Delta x\) then

  • the differential \(d y\) is defined by \(d y=f^{\prime}(x) d x\) and is the change in the tangent line.

  • the corresponding small change in the function is \(\Delta y \approx d y\).

Hence \(\Delta y \approx f^{\prime}(x) \Delta x\) and \(f(x+\Delta x) \approx f(x)+f^{\prime}(x) d x\).

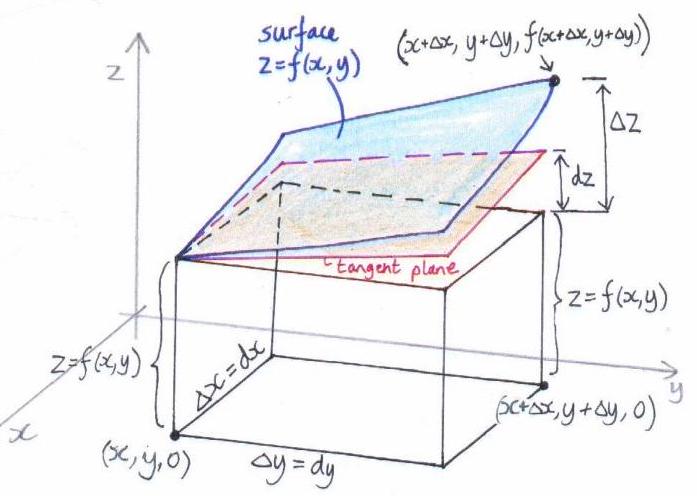
Similarly, suppose we have a differentiable function \(z=f(x, y)\) and that \(x\) and \(y\) change by amounts \(d x=\Delta x\) and \(d y=\Delta y .\)

  • The total differential \(d z\) is defined by \(d z=f_{x}(x, y) d x+f_{y}(x, y) d y=\frac{\partial f}{\partial x} d x+\frac{\partial f}{\partial y} d y\) and is the change in the tangent plane.

  • The change in the function is \(\Delta z\). For small changes, \(\Delta z \approx d z=f_{x} \Delta x+f_{y} \Delta y\) and \(f(x+d x, y+d y) \approx f(x, y)+d z=f(x, y)+f_{x}(x, y) d x+f_{y}(x, y) d y\).

../../../_images/img1.jpg

Extensions to higher dimensions#

Linearizations and differentials can be defined in a similar way for functions of more variables. For example, for \(w=f(x, y, z)\)

  • the linear approximation of \(f\) at \((a, b, c)\) is \(f(x, y, z) \approx L(x, y, z)=f(a, b, c)+f_{x}(a, b, c)(x-a)+f_{y}(a, b, c)(y-b)+f_{z}(a, b, c)(z-c) .\)

  • the differential \(d w\) is \(d w=f_{x} d x+f_{y} d y+f_{z} d z\).

Note on Differentiability#

Differentiability of functions of two or more variables is more complicated.

  • Informally it can be said that a function \(f(x, y)\) is differentiable at a point \((a, b)\) if it is wellapproximated by a linear function near that point.

  • More formally, it can be proved that if the partial derivatives \(f_{x}\) and \(f_{y}\) exist and are continuous on a small disk centred at \((a, b)\) then \(f\) is differentiable at \((a, b)\).