Directional Derivatives and Gradient Vector#

Gradient Vector#

For a differentiable function \(f(x, y)\), the gradient vector is defined by

\[ \vec{\nabla} f=\operatorname{grad} f=\left\langle f_{x}, f_{y}\right\rangle=\frac{\partial f}{\partial x} \mathbf{i}+\frac{\partial f}{\partial y} \mathbf{j} \]

Directional Derivative#

The directional derivative of \(f(x, y)\) at \((a, b)\) in the direction of a unit vector \(\hat{\boldsymbol{u}}=\left\langle u_{1}, u_{2}\right\rangle\) is, provided the limit exists,

\[ D_{\vec{u}} f(a, b)=\lim _{h \rightarrow 0} \frac{f\left(a+h u_{1}, b+h u_{2}\right)-f(a, b)}{h} . \]

Hence the directional derivative of a differentiable function \(f(x, y)\) at \((a, b)\) in the direction of a unit vector \(\hat{\boldsymbol{u}}=\left\langle u_{1}, u_{2}\right\rangle\) is

\[ D_{\vec{u}} f(a, b)=\overrightarrow{\boldsymbol{\nabla}} f(a, b) \cdot \hat{\boldsymbol{u}}=f_{x}(a, b) u_{1}+f_{y}(a, b) u_{2} . \]

It is the rate of change of \(z\) in the direction of \(\hat{\boldsymbol{u}}\) (and is a scalar)
Alternative notations: \(\left.D_{\vec{u}} f\right|_{(a, b)}, \quad f_{\vec{u}}(a, b)\)

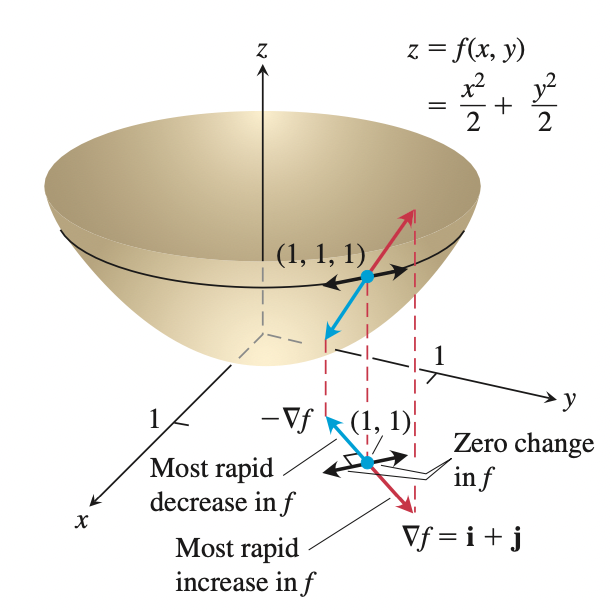
Geometrical properties#

If \(f\) is a differentiable function at the point \((a, b)\) and \(\vec{\nabla} f(a, b) \neq \overrightarrow{\mathbf{0}}\), then:

\(\vec{\nabla} f(a, b)\) is perpendicular to the level curve (contour) of \(f\) through \((a, b)\)
the maximum rate of change of \(f\) at \((a, b)\) is \(|\vec{\nabla} f|\) and occurs in the direction of \(\vec{\nabla} f(a, b)\).

Functions of 3 Variables#

Similarly for a function \(f(x, y, z)\), the gradient vector is defined by

\[ \vec{\nabla} f=\operatorname{grad} f=\left\langle f_{x}, f_{y}, f_{z}\right\rangle=\frac{\partial f}{\partial x} \mathbf{i}+\frac{\partial f}{\partial y} \mathbf{j}+\frac{\partial f}{\partial z} \mathbf{k} \]

The directional derivative of \(f(x, y, z)\) at \((a, b, c)\) in the direction of a unit vector \(\hat{\boldsymbol{u}}=\) \(\left\langle u_{1}, u_{2}, u_{3}\right\rangle\) is

\[ D_{\vec{u}} f(a, b, c)=\overrightarrow{\boldsymbol{\nabla}} f(a, b, c) \cdot \hat{\boldsymbol{u}}=f_{x}(a, b, c) u_{1}+f_{y}(a, b, c) u_{2}+f_{z}(a, b, c) u_{3} . \]

If \(\overrightarrow{\boldsymbol{\nabla}} f(a, b, c) \neq \overrightarrow{\mathbf{0}}\), then:

\(\vec{\nabla} f(a, b, c)\) is perpendicular to the level surface of \(f\) at \((a, b, c)\)
the maximum rate of change of \(f\) at \((a, b, c)\) is \(|\vec{\nabla} f|\) and occurs in the direction of \(\vec{\nabla} f(a, b, c)\).