Triple Integrals#

Triple integral on a box#

Consider a function \(f(x, y, z)\) continuous on a box \(B=[a, b] \times[c, d] \times[r, s]\).

We can define a triple Riemann sum and triple integral:

\[ \iiint_{B} f(x, y, z) d V=\lim _{m, n, p \rightarrow \infty} \sum_{i=1}^{m} \sum_{j=1}^{n} \sum_{k=1}^{p} f\left(x_{i j k}^{*}, y_{i j k}^{*}, z_{i j k}^{*}\right) \Delta V . \]

The triple integral can be evaluated by using iterated integrals and ‘partial integration’: integrating with respect to one variable while holding the other two variables constant.

\[ \iiint_{B} f(x, y, z) d V=\int_{a}^{b} \int_{c}^{d} \int_{r}^{s} f(x, y, z) d x d y d z \]

Triple integrals on general regions#

Suppose region \(E\) lies between surfaces \(z=u_{1}(x, y)\) and \(z=u_{1}(x, y)\), and that \(D\) is the projection of \(E\) onto the \(x y\)-plane, so

\[ E=\left\{(x, y, z):(x, y) \in D, u_{1}(x, y) \leq z \leq u_{2}(x, y)\right\} \]

then

\[ \iiint_{E} f(x, y, z) d V=\iint_{D}\left(\int_{u_{1}(x, y)}^{u_{2}(x, y)} f(x, y, z) d z\right) d A . \]

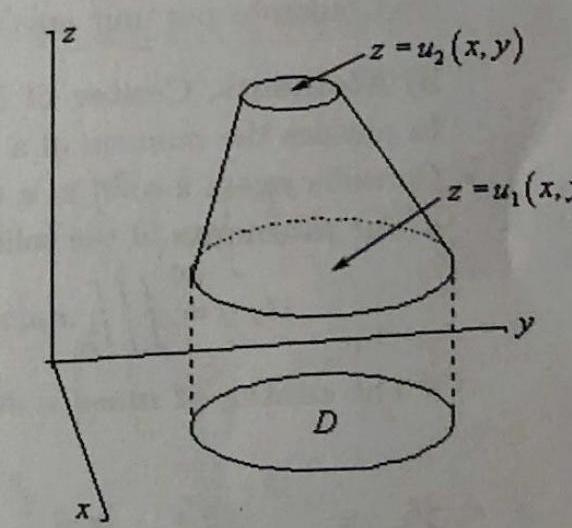
If \(D\) is a type I region, \(D=\left\{(x, y): a \leq x \leq b, g_{1}(x) \leq y \leq g_{2}(x)\right\}\), then

\[ \iiint_{E} f(x, y, z) d V=\int_{a}^{b} \int_{g_{1}(x)}^{g_{2}(x)} \int_{u_{1}(x, y)}^{u_{2}(x, y)} f(x, y, z) d z d y d x . \]

(Alternatively D may be type II or may be best described using plane polar coordinates.)

Iterated integrals can be written in a similar way for other situations.

Constructing and evaluating triple integrals#

  • Determining the limits of integration is usually the most difficult step!

  • When possible, it is helpful to sketch two diagrams:

    • A diagram of the 3D region.

    • Sketch of the 2D projection of the region onto the xy-plane (or other plane, as appropriate).

  • There is often more than one way of writing the integral … but one form may be easier to evaluate than others.

Note: The limits on the outermost integral must be constants. The limits on inner integrals can be only in terms of the remaining variables.

Further applications of multiple integrals#

Density and Mass#

  • Suppose a solid occupies a region \(E\) and the density (mass per unit volume) varies with position according to the function: \(\rho(x, y, z)\). A differential volume element \(d V\) at \((x, y, z)\) will have mass \(d m=\rho(x, y, z) d V\). The total mass of the solid is therefore \(m=\iiint_{E} \rho(x, y, z) d V\).

  • Similarly for a thin, flat plate in a region \(D\) of the \(x y\)-plane we can consider (areal) density (mass per unit area): \(\rho_{s}(x, y)\). A differential area element \(d A\) at \((x, y)\) will have mass \(d m=\rho_{s}(x, y) d A\). The mass of the plate will therefore be \(m=\iint_{D} \rho_{s}(x, y) d A\).

  • The ideas above can be extended to other types of densities. For example, if electric charge is distributed in a 3D region \(E\) we may consider the charge density \(\sigma(x, y, z\) ) (in Coulombs per unit volume). The total charge in region \(E\) will be \(Q=\iiint_{E} \sigma(x, y, z) d V\). Or if electric charge is distributed over a 2D surface \(D\) with surface charge density \(\sigma_{s}(x, y)\) (in Coulombs per unit area), the total charge will be \(Q=\iint_{D} \sigma_{s}(x, y) d A\).

Moments, Center of Mass and Centroid#

In physics the moment of a particle with mass \(m\) about an axis at a distance \(r\) is \(m r\).

Consider again a solid in a region \(E\) with density \(\rho(x, y, z)\).

  • The moments of the solid about the three coordinate planes are

\[ M_{Y Z}=\iiint_{E} x \rho(x, y, z) d V, \quad M_{X Z}=\iiint_{E} y \rho d V, \quad M_{X Y}=\iiint_{E} z \rho d V . \]

  • The center of mass is at \((\bar{x}, \bar{y}, \bar{z})\) where

\[ \bar{x}=\frac{M_{Y Z}}{m}, \quad \bar{y}=\frac{M_{X Z}}{m}, \quad \bar{z}=\frac{M_{X Y}}{m} \]

and \(m\) is the total mass of the solid (found by the integral given in i) above).

  • For a solid of uniform density, the center of mass is called the centroid. That is, the centroid of the solid is at \((\bar{x}, \bar{y}, \bar{z})\) where \(\bar{x}=\frac{M_{Y Z}}{m}=\frac{1}{m} \iiint_{E} x d V\), etc.

Probability#

  • (Review) The probability that a single continuous random variable \(X\) takes values between \(a\) and \(b\) is found by evaluating an integral \(P(a \leq X \leq b)=\int_{a}^{b} p(x) d x\) where \(p\) is a probability density function and has the properties \(\quad p(x) \geq 0 \quad \forall x \quad\) and \(\int_{-\infty}^{\infty} p(x) d x=1\).

In this case the mean or expected value, of \(X\) is \(\mu=\int_{a}^{b} x p(x) d x\).

  • Similarly, if we have two continuous random variables \(X\) and \(Y\) then the probability that \((X, Y)\) take values lying in a particular region \(R\) is found by evaluating an integral \(P((X, Y) \in R)=\iint_{R} p(x, y) d A \quad\) where \(p(x, y)\) is a joint probability density function and has the properties \(p(x, y) \geq 0\) and \(\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} p(x, y) d x d y=1\)

The expected values of \(X\) are \(Y\) are

\[ \mu_{X}=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} x p(x, y) d x d y \quad \text { and } \quad \mu_{Y}=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} y p(x, y) d x d y \]